《深度学习详解》--1、通过案例了解机器学习
DataWhale X 李宏毅苹果书 AI夏令营
Introduction of Machine / Deep Learning
基础概念
近些年,人工智能飞速发展,我们经常听到人工智能、机器学习、深度学习和强化学习等名词。事实上,它们之间存在着密切的联系。
人工智能
人工智能(Artificial Intelligence, AI)是一个广泛的领域,可以从“能力”和“学科”两个方面对人工智能进行定义。从能力的角度看,人工智能是指用人工的方法在机器上实现的智能;从学科角度看,人工智能是一门研究如何构造智能机器或智能系统,使其能模拟、延伸和扩展人类智能的学科。
机器学习
机器学习(Machine Learning, ML)是AI的一个子集,它专注于开发算法和统计模型。机器学习是指在不需要明确编程的情况下,让计算机能够利用数据提高在某个任务上表现的算法。机器学习又可以分为监督学习、无监督学习、半监督学习和强化学习等。
深度学习
深度学习(Deep Learning, DL)是机器学习的一个子领域,它使用类似于人脑的神经网络结构,特别是具有多个层的深层神经网络,来学习复杂的模式和表示。
强化学习
强化学习(Reinforcement Learning, RL)是机器学习的一个分支,它专注于如何让智能体(agent)通过与环境的交互来学习最佳行为或策略,以最大化某种累积奖励。
深度强化学习
深度强化学习(Deep Reinforcement Learning, DRL)是深度学习和强化学习的结合,它使用深度神经网络作为智能体的大脑,以处理高维度的输入数据并学习复杂的策略。
课程基础
机器学习
机器学习最重要的是寻找到一个函数,让机器具备找到一个函数的能力。
通常情况下,函数是非常复杂的,人难以自己写出,若是通过机器的力量自己找出有很多优势。
机器学习寻找的函数通常是不同的,根据实际需求可以分成回归、分类和结构化学习等。
回归(regression)
假设要找的函数输出的是一个数值,或者称为一个标量(scalar),这种机器学习的任务称为回归。(根据历史数据和指标预测未来的一个数值)
回归问题中,比较经典的是房价预测问题,这个问题在很多教程中都被作为例子,在Kaggle中可以进行实践。
分类(classification)
分类任务是让机器做选择题,函数的输出是从设定好的选项中选出一个选项当作输出。通常,在确定选项的过程中会牵扯到概率的计算,根据概率判断最可能的选项,常见的分类算法中都有概率的影子,个人感觉人工智能技术的发展确实离不开数学的支持。
在分类问题中,比较常见的就是垃圾邮件判断的例子,判断邮件是否为垃圾邮件,这是一个二分类问题,除此之外还有多分类,AlphaGo下围棋就是从棋盘中找到最正确的选项,还有动物识别(猫、狗、鸟……)。
结构化学习(structed learning)
在这种情况下,机器学习并不只是要做出选择或者输出一个数字,而是要产生一个有结构的物体,比如画一张图、写一篇文章……近些年也逐渐得到更多应用。 在其他学习群里看到过一张有意思的图: 
结构化学习仍需要我们去探索。
案例学习
已有的数据是youtube后以往的信息,想要得到的明天可能观看的次数是多少 通过一个函数来实现这个过程
机器学习找函数的过程
1、写出一个带有未知参数的函数(这个函数基于我们的知识积累设置,这只是一个猜测),这个函数能够预测未来观看的次数
\[y=b+wx_1\]其中$y$表示要预测的观看次数,$x_1$ 表示前一天的观看人数
$w$和$b$都表示未知的参数,都需要让机器从数据中学习
2、定义损失函数(loss function)
损失函数就是:在当前参数组合下,所有数据误差和的平均值(个人理解),公式如下:
\[L= \frac{1}{N} \sum_n^{i=1} e_n\]其中$e$表示误差
可以采用预测值与目标值之间差的绝对值:$e = \vert y - \hat{y} \vert$
也可以采用差的平方: $e=(y-\hat{y})^2$
当采用绝对值,称为MAE(Mean Absolute Error)
当采用平方,称为MSE(Mean Squared Error)
除了上述的两种方式,还有一种计算loss的方式称为“交叉熵”
计算的损失函数可以通过可视化方式呈现,如:热力图、等高线图……。下面是课程中采用的示例: 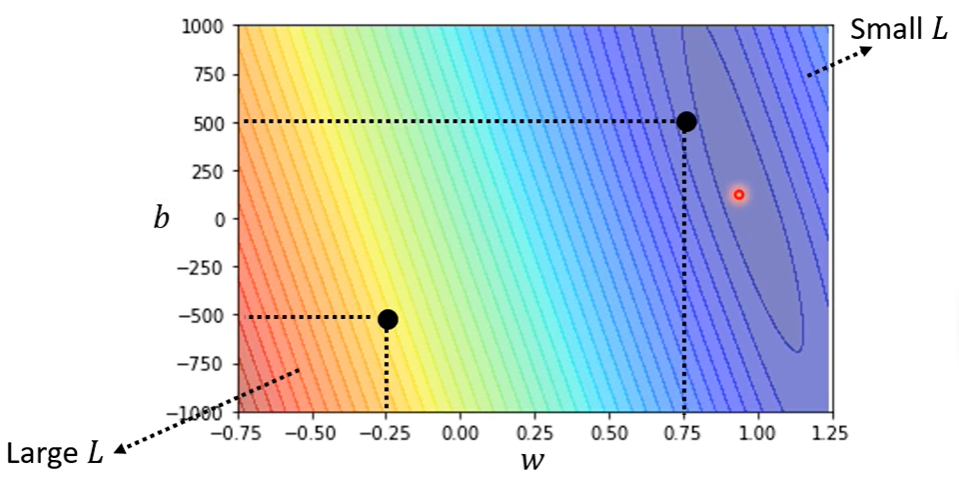
3、优化(Optimization)
优化的目的是让损失函数的值最小,如下公式:
\[w^*,b^*=min_{w,b}L\]我们要找到让损失函数值最小的未知参数组合。
常用的方式是梯度下降(gradient descent),通过梯度下降进行参数优化的过程如图: 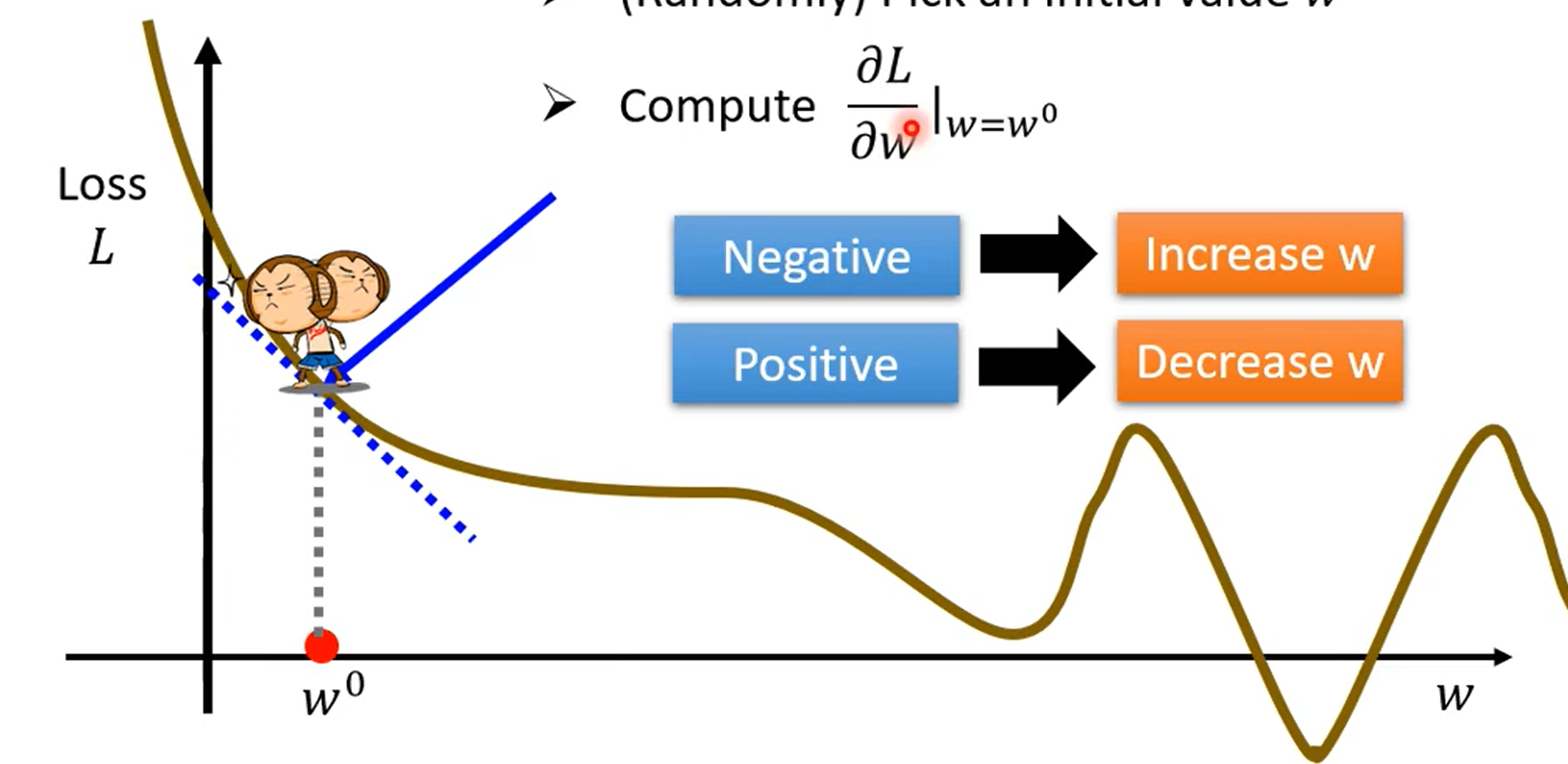
其中有几个非常重要的概念:
斜率:斜率大于0表示loss在上升,斜率小于0表示loss在下降,等于0表示到达了一个极值点。
学习率(learning rate):$\eta$可以理解为跨一步的大小,$\eta$越高,跨一步越大,反之越小。$\eta$可以经验决定。
超参数(hyperparameter):在机器学习过程中需要人为预先设定的参数。
还有一个重要的点是关于$w$的更新: \(w^1 \leftarrow w^0 - \eta \frac{\partial{l}}{\partial{w}}\vert_{w=w^0}\)
随着$w$的不断更新,理想状态下loss的斜率会成为0,如下图所示 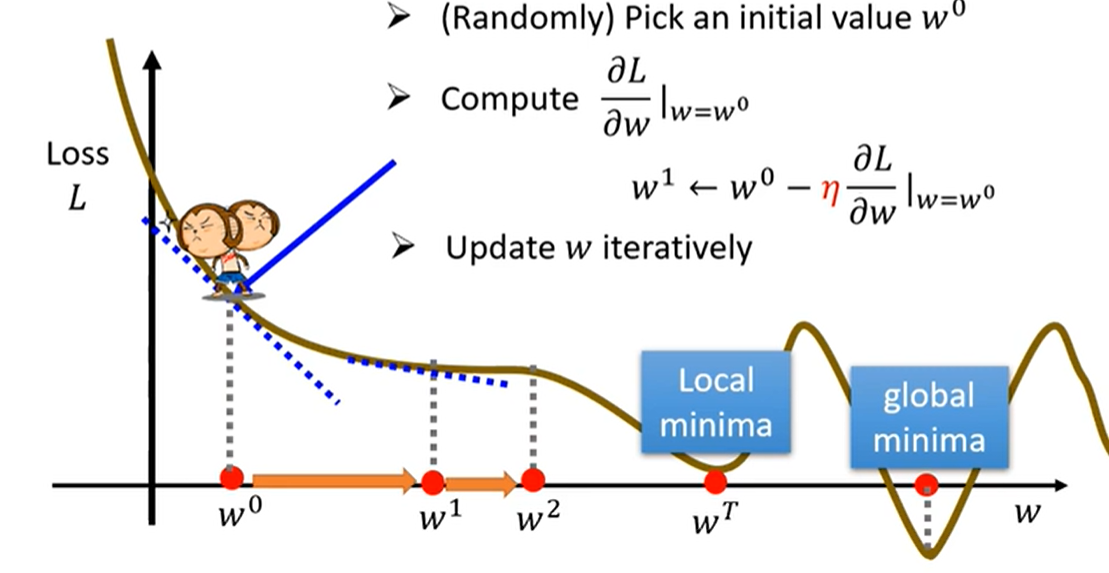
当$w=w^T$时,斜率为0,当时此时loss并不是最低的
local minima:局部最小
global minima:全局最小
在上图中,一个有意的现象,loss有负值,为什么loss可以是负的?
因为loss是可以自己定义的,用上边的绝对值和平方计算肯定是正值,但是如果自己定义不同的方式可以是负值。
4、最后
找到合适的模型要观察数据、理解数据并进行试验,根据结果更新模型。
